「統計」這個名詞的意義因人而異,對一般人而言,統計是任何方面專家們用以支持其論點的一大堆數字;對於略具常識的人來講,這個名詞代表用以摘要和解釋一堆數據如計算平均數 (mean) 與標準差 (Standard deviation) 的程序之類的概念。但是對於從事統計工作的人員而言,統計是依小量數據(樣本)所提供的資料以估計預測某研究對象如群體的方法。或者更廣義地說,統計為面對不定狀況制定決策提供方法的科學。
雖然統計的起源可追溯至十八世紀甚至更早,然而統計學主要的發展卻遲至十九世紀末葉二十世紀初期才真正開始。到了四十年代才逐漸成熟,統計學和機率論的關係異常密切,事實上任何統計問題的研究都必須牽涉到機率論的運用,因為後者實為前者的主要工具。
統計人員對如下所舉之類問題的答案深感興趣:是否接受本批送驗成品?吸煙與得癌症有關嗎?張三會於下屆選舉中獲勝嗎?為了回答上述問題,我們必須由具「代表性」的特殊狀況以「瞭解」一般的狀況,由樣本「推測」群體。因此,由統計人員所推測得到的結論都不是絕對肯定可以接受。事實上,統計人員的職責之一是量度他所得結論肯定的程度,但是我們不能以為統計的缺乏肯定性而誤認為統計數學不嚴密,因為構成統計基礎的數學是機率論,它有固若磐石的數理化基礎和經嚴密證明的定理。
一般而言,我們可以把統計問題分成兩類: 敘述統計和推論統計,簡單的說:任何對數據(即樣本)的處理導致預測或推論群體的統計稱為推論統計。反之,如果我們的興趣只限於手頭現有的數據,而不準備把結果用來推論群體則稱為敘述統計。舉個例子來說,依據過去十年來的統計,每年來華觀光的人數,平均每人在臺停留的日數,平均每人每天在華的花費,十年內那一年創最高記錄等等都是屬於敘述統計的範圍;但是如果我們根據這些年所得的數據來預測來年可能的觀光客人數就是推論統計的問題了。十年前的初級統計課本大多談敘述統計,如今由於計算機的盛行,這部份的工作大多利用計算機來解決,稱為數據處理,而一般統計書的重點別放在推論統計。
大致說來,推論統計分為三大類,就是估計,檢定和分類與選擇。譬如說,張三想競選臺北市議員,他想估計一下可能有多少人會投票給他,於是他以隨機抽樣的方式,詢問100位有投票權的市民的意見,而後根據所得結果推論可能全市有多少人會選他,這是估計問題。又如某家庭主婦想知道她心中懷疑潔王牌洗衣粉的洗淨力是否比愛王牌洗衣粉強,首先假設潔王牌比愛王牌好,然後經過試驗來測定這假說是否成立,在本例中,我們並不想估計任何參數,而只是想檢驗事先所敘述的假設是否成立其可靠性有多大,這就是檢定問題。還有,新製造的三種藥品中那幾種比目前所用的這種藥品有效呢?這是選擇的問題。如果我們把統計設想為經由抽樣以制定決策的科學,那麼我們似乎宜以十九世紀末期高爾頓爵士(Sir Francis Galton, 1822~1911)和卡爾.皮爾遜(Karl Pearson, 1857~1936)的論述做為它的起點。從那時開始,現代統計理論的發展可略分為四大思潮,在這四大時期,每一階段都是以一位偉大的統計學家的專著為先導 。
第一階段隨著1899年高爾頓的《Nature Inheritance》一書的出版而展開序幕,該書除了其本身的價值外,還引發了傑出的統計學家卡爾.皮爾遜對統計學的興趣。在此之前,皮氏只是在倫敦大學的大學部 (University College) 執教的數學教員。當時,這「所有知識都基於統計基礎」的想法引起了他的注意。
1890年他轉到格里辛學院 (Gresham College),在那裏他可講授任何他希望講授的課程,皮氏選了一個題目「現代科學的範圍與概念」(the Scope and Concepts of modern Science) 在他的授課中他越來越強調科學定律的統計基礎,後來他全神集中致力於統計理論的研究。不久他的實驗室成為世界各地人們學習統計和回國點燃「統計之火」的研究中心。經由他熱心的提倡,科學工作者逐漸由對統計研究不感興趣的境地轉而成為熱切地努力發展新理論和搜集並研究得自各方面的數據。人們越來越深信統計數據的分析能為許多重要的問題提供解答。
海倫.華克 (Helen Walker) 描述皮氏小時候的一則軼事,生動地顯示他往後事業中所表現的特色 註2 。有人問皮爾遜他所記得最早的事,他說「我不記得那時是幾歲,但是我記得是坐在高椅子上吸吮著大拇指,有人告訴我最好停止吮它,不然被吮的大拇指會變小。我把兩手的大拇指並排看了很久,它們似乎是一樣的,我對自己說:我看不出被吸吮的大拇指比另一個小,我懷疑她是否在騙我」。
在這個單純的故事中,海倫華克指出「不盲信權威,要求實證,對於自己對觀測數據的意義的解繹深具信心,和懷疑與他的判斷不同的人態度是否公平」這些就是皮氏一生獨具的特徵。
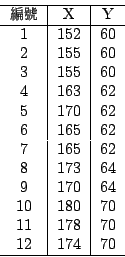
這個第一階段的特點就是人們對統計的態度轉變了,統計的重要性被科學界所承認。除此之外,在統計技巧上也有很多的進展,我們利用上面這個十二個人的身高和體重的數值表介紹一些最基本的統計觀念,其中身高 X 以公分為單位,體重 Y 以公斤為單位。
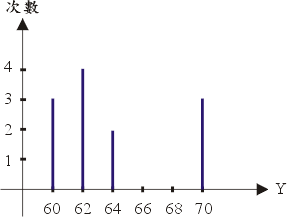
圖一 |
為了對這組資料得到一點概念,我們把它列成圖形。英人普萊菲(William Playfair, 1759~1823)被公認為將圖形表示的概念介紹到統計學的第一人。他的著作,大多為關於經濟學,多採用圖形如直方圖、條形圖。在我們上述問題中,用次數圖就能很清楚地表示出來,圖一就是身高 X 的次數圖,體重 Y 的次數圖也很容易表示。有興趣的讀者不妨一試。雖然這類圖形能幫助我們的直覺,但是如果想對這些數據更一步瞭解,我們必得進一步用某些量來描述它們。在這類數量中最重要之一是對於集中趨勢的測度。最早的集中趨勢的測度實際上可追溯至古希臘,是算術平均數 ![]() ,即
,即
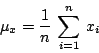
其中 xi 代表變數 X 的數值,n 為觀測值的總個數,計算結果得到身高的平均數
其中 fj 是 xj 出現的次數,並對不同的 X 變數 xj 值求和。
假設有一根無重的木桿,其上刻著變數 Y 的各不同值的刻度,並且設想在 xj 處掛著質量 ![]() 的物品,則整個體系的質量為 1,而
的物品,則整個體系的質量為 1,而 ![]() 為質量重心,也就是說如果把支點設於
為質量重心,也就是說如果把支點設於 ![]() ,則整個體系會趨於平衡,以本例的身高而言,其體系如圖二所示。
,則整個體系會趨於平衡,以本例的身高而言,其體系如圖二所示。
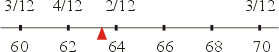
圖二 |
這種對平均數的解釋在以後我們思考連續分配觀念時,很有幫助。
雖然中位數 (median) 觀念可能早已有之,但是遲至1883年才經由高爾頓把它引入統計,成為集中趨勢第二種測度。所謂中位數就是所有觀測值依大小排起來,中間的那個數,若是偶數個數就是兩個中間數的平均數,在我們例子中身高的中位數為165。
另外還有一個集中趨勢的測度是眾數,1894年左右由卡爾.皮爾遜所介紹。眾數如果存在的話,就是出現次數最頻繁的數值,如果兩個或兩個以上的數值出現次數相同,眾數就不太有意義了,在我們例子中體重的眾數是62。
如果變數 X 的分配是完全對稱,即其次數圖完全地對稱於一垂直線,那麼平均數、中位數和眾數(如有一眾數存在的話)會重合為一點。讀者們應注意,反過來說並不成立。也就是說不對稱的圖形也可有平均數,中位數和眾數重合的情形(即平均數、中位數和眾數重合並不保證圖形為對稱)。
對大多數的目的而言算術平均數是最常用的集中趨勢測度,這當然有它學理上的意義。雖然有時候計算相當費時,中位數也有它的優點,它不受少數極端值的影響。例如在我們的例題中,若把一個身高180公分的人換成一個200公分的人,平均數就會受到很大的影響,而中位數卻全然不變。
其次我們談一下「離差」(dispersion) 的測度,它是數據以平均數為準對於分散程度的測度。最早這種測度大概是貝塞(Bessel)於1815年用於有關天文學問題的「可能誤差」。目前最通用的是「標準差」σ,這個名詞是1894年卡爾.皮爾遜所創。
離散變數 X 的標準差定義為
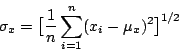
由這個公式可以看出若數據非常分散,
為了介紹相關的觀念,我們回頭再仔細看一下表一中的身高和體重,數值顯示這兩個變數似乎有某種相關存在,根據常識,高的人通常要比矮的人重,在這些數據點繪在直角坐標的平面上,可以看出它們之間的關係,稱為分佈圖(參見圖三),如果它們之間為線性關係,則點的趨向會呈現在直線的附近。
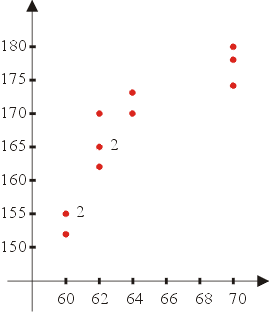
圖三 |
~~~摘錄自戴久永的文章,全文請參閱原網址http://episte.math.ntu.edu.tw/articles/mm/mm_03_3_09/index.html




 留言列表
留言列表


 {{ article.title }}
{{ article.title }}