呈本系列第一篇文章所提及,競爭風險存活分析目前主流方法有二,特定因素危險函數(Cause-Specific Hazard Function,以下簡稱CSH)與次分佈瞬間危險(SubDistribution HazardFunction,以下簡稱SDH),本篇將介紹CSH的概念與背後的想法。讀者必須要先瞭解傳統存活分析對於風險集(Risk set)的算法,特別是最常用的Kaplan-Meier(KM)的估算方法,讀者可參考筆者之前介紹KM法的文章(短網址:goo.gl/HtM58w)。
CSH是由Cox model所變化而成,風險集的設定也是採取Kaplan-Meier的估算方法:一旦發生研究興趣事件或是失去追蹤(設限,censor)的個案,在下一個觀察時間,皆從觀察名單中(Populationat risk/ patient at risk)被排除。如圖2所示,Time=1時觀察名單有30人,且同時興趣事件(正方形□)發生1位,競爭風險(三角形▲)發生1位。於是在Time=2時,上一個時間點已發生興趣事件及競爭風險的人皆從觀察名單中被排除,故計算Time=2的危險函數(Hazard function)時,觀察名單為30-1-1=28人。
(圖片來源:Lau B, Cole SR, Gange SJ. Competing risk regression models for epidemiologic data. American journal of epidemiology 2009; 170:244-256.)
由圖2可知,CSH與Coxmodel的差別僅在於前者允許存在多個事件。CSH除了需符合Coxmodel的假設之外,額外有一項「獨立設限」(Independent censoring)的假設,亦即CSH假設所有設限事件是獨立無相關的(在這裡指的是各項競爭風險之間是沒有相關性的)。目前並沒有方法可以檢定資料形態是否符合獨立設限的假設,僅能以敏感度分析(Sensitivity analysis)的方式,假設全部皆無發生競爭風險,以及假設全部皆發生競爭風險之下的存活分析。
從上述例子中,可知CSH對於競爭風險仍是以設限方式處理,看似與Cox model並無不同,但是對於死亡事件之外的其他競爭風險就能看出兩者之間的差異。以前述膀胱癌復發的例子來說(圖3),根治性膀胱全切除手術(病人編號1號)的人,雖然在Cox model與CSH中皆是設限狀態,但是兩種模式的追蹤時間的算法並不同。CSH的追蹤時間在病人發生競爭風險的當下便停止追蹤,即追蹤時間為t1。而Cox model的追蹤時間是到病人發生研究興趣事件或是研究終止,因此此人在Cox model中,是直到研究終止才變成設限狀態,即追蹤時間為t1+t2。
圖3、Cause-specific hazard function發生競爭風險(除了死亡事件之外)的追蹤時間算法
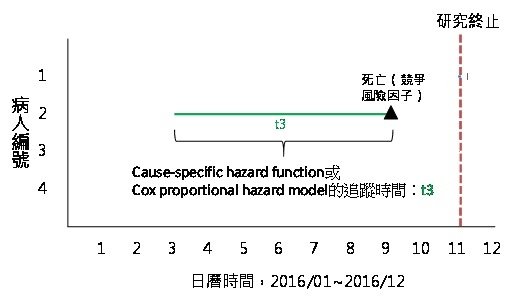
而編號2號的病人,發生的競爭風險因子為死亡事件,無論是CSH發生競爭風險的當下便停止追蹤,或是Cox model追蹤到研究終止或死亡時,兩者的追蹤時間皆為死亡事件發生當下的時間,如圖4所示,其追蹤時間等於t3。由此可知,當研究的競爭風險僅有死亡一項因子時,CSH與Cox model會得到相同的結果。
圖4、Cause-specific hazard function發生死亡競爭風險的追蹤時間算法






 留言列表
留言列表


 {{ article.title }}
{{ article.title }}