筆者前陣子分享過一篇(使用G-power計算RCT介入研究所需樣本數),此篇將繼續延伸此議題,若研究者在撰寫樣本數規劃時,希望在公式方面能夠有所依據的話,不妨參考此篇的介紹,也提供自己多一點選擇,這篇所參考的資料來源是Hedeker, Gibbons, & Waternaux (1999). Sample size estimation for ongitudinal designs with attrition. Journal of Educational and Behavioral Statistics, 24:70-93。
文章主要介紹效果量與樣本數的計算公式,也提到之前筆者介紹的Diggle公式,但上次有提到Diggle的公式比較兩組在平均時間(time-averaged)的差異,但像GEE或是HLM在檢驗介入效果時,是利用交互作用項去檢驗兩組改變量的差異,在概念上顯然明顯不同,因此本篇將介紹另一個公式Comparing two groups across timepoints - balanced case(Overall and Doyle, 1994),通常介入研究的樣本數規劃會假設兩組是相等的,因此本文章也只針對這個條件做介紹。
μ1i – 實驗組在time i的平均數、μ2i – 對照組在time i的平均數
σi2 – outcome在各時間點的變異數(不分組別,合併計算)
σij – outcome在任兩時間點間的共變異數(不分組別,合併計算)
ci – 對比係數,當只有兩個時間點時c1 = -1,c2 = 1

透過公式可以知道,想從其他文獻得到所有公式內需要的參數相當困難,因此這樣的公式適合在以下幾種情形。
1.已經完成統計分析,並需要計算介入結果的效果量
2.先進行小型的先趨研究(pilot study),計算其效果量為何,進而計算所需樣本數,最後再本所需樣本補齊
因此我們需要下列幾項參數值:a.兩組個別在前測與後測的平均數,或是兩組在前測及後測的個別差值;b.前測與後測個別的變異數(兩組合在一起);c.前後測的相關係數(兩組合在一起),以下透過SPSS作介紹。
(1)點選「分析」→選擇「比較平均數法」→選擇「平均數」。
(2)將前測與後測放入「依變項清單」。
(3)將組別放入「自變項清單」。
(4)得到兩組分別在前測與後測個別的平均數。
(5)透過Excel,進一步計算兩組在前測的差值及後測的差值。
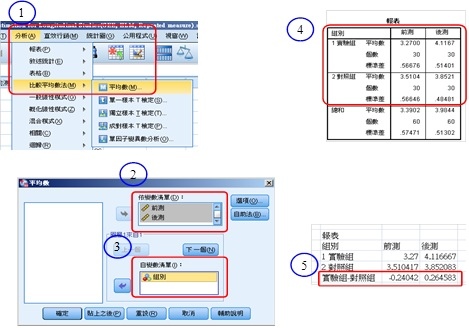
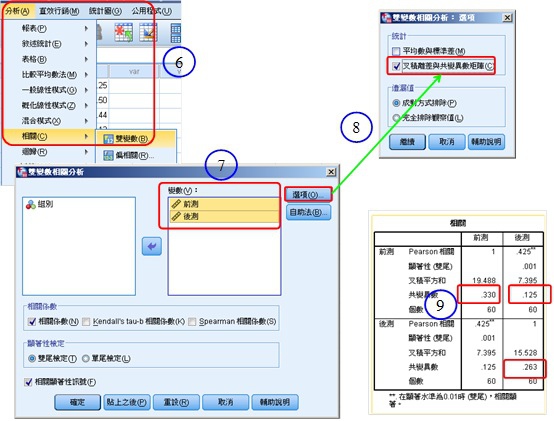
(6)點選「分析」→選擇「相關」→選擇「雙變數」。
(7)將前測與後測放入「變數」。
(8)點選「選項」→選擇「積叉離差與共變異數矩陣」。
(9)得到前測的變異數、後測的變異數及前後測的共變異數。
(10)計算效果量
效果量δ = (Ψc) / (σc) =
Ψc = (-1)*(兩組前測差異) + (1)*(兩組後測差異)
= (-1)*(-0.24024) + (1)*(0.264583) = 0.505
σc2 = (-1)2*(前測變異數)+(1)2*(後測變異數)+2*(-1)*(1)*(前後測共變異數)
= (0.330297)+(0.263192)-2*(0.125334) = 0.34282
因此效果量δ=0.505 / 0.34282 = 1.473075
(11)計算樣本數
樣本數n = 2(Zα+Zβ)2/δ2
在設定α = 0.05,雙尾檢定時,Z = 1.96
在設定β = 0.2,Z = 0.842
因此樣本n = 2(1.96+0.842)2/(1.473075)2 = 7.2363 [2019-11-6 勘誤]




 留言列表
留言列表


 {{ article.title }}
{{ article.title }}