PIXNET Logo登入

晨晰統計部落格新站（統計、SPSS、BIG DATA討論園地）

跳到主文

一個討論統計的好地方

部落格全站分類：圖文創作

  • 相簿
  • 部落格
  • 留言
  • 名片
  • 10月 27 週一 202509:11

  • 醫學研究使用PowerBI的情境(2)—介入措施


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(26)

  • 個人分類：生物醫學統計
▲top
  • 9月 22 週一 202509:20

  • 醫學研究使用PowerBI的情境(1)—製作圖表


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(36)

  • 個人分類：生物醫學統計
▲top
  • 7月 14 週一 202511:02

  • 時間相依Cox model：以生物製劑對帶狀皰疹風險之影響為例

時間相依Cox model：以生物製劑對帶狀皰疹風險之影響為
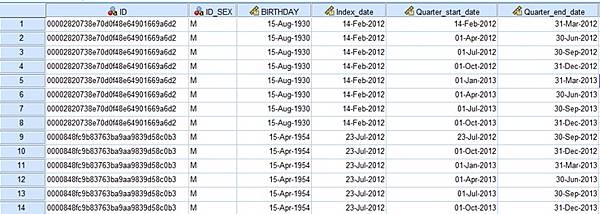
一、前言
在醫療研究領域中，許多重要的問題與事件（如中風、癌症復發、死亡）都與「時間」息息相關。傳統的 Cox 比例風險模型（Cox Proportional Hazards Model）假設暴露變項於追蹤期間維持不變，然而，現實中許多情境（如藥物使用、環境暴露）其實會隨時間變動。這時，便需使用「時間相依（time-dependent）」的存活分析方法，以避免錯誤推論。
(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(75)

  • 個人分類：生物醫學統計
▲top
  • 4月 28 週一 202509:13

  • 為什麼醫療業也要做問卷？3 大問卷應用情境


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(20)

  • 個人分類：生物醫學統計
▲top
  • 1月 20 週一 202511:19

  • EHJ高分論文分享


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(42)

  • 個人分類：生物醫學統計
▲top
  • 5月 13 週一 202409:16

  • 當倚天劍遇上屠龍刀：GEE與mixed model大PK


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(55)

  • 個人分類：生物醫學統計
▲top
  • 4月 15 週一 202411:17

  • 生物醫學統計不可不會的混合模式（mixed model）


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(138)

  • 個人分類：生物醫學統計
▲top
  • 3月 18 週一 202409:03

  • 生物醫學統計必須搞懂的GEE（廣義估計方程式）


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(154)

  • 個人分類：生物醫學統計
▲top
  • 11月 20 週一 202309:11

  • 深度剖析美兆健檢資料庫，量身打造最適合的研究主題


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(81)

  • 個人分類：生物醫學統計
▲top
  • 11月 13 週一 202309:03

  • 美兆健檢資料庫+800題個人生活調查=黃金論文


(繼續閱讀...)
文章標籤

晨晰部落格新站 發表在 痞客邦 留言(0) 人氣(103)

  • 個人分類：生物醫學統計
▲top
12...16»

2023社群金點賞

晨晰主打星

個人資訊

晨晰部落格新站
暱稱：
晨晰部落格新站
分類：
圖文創作
好友：
累積中
地區：

熱門文章

  • (141,481)因果關係的第三者-中介變項（Mediator / Mediation）-上～晨晰統計林星帆顧問整理
  • (111,625)變異數不同質的處理
  • (110,263)透過G-power軟體計算迴歸分析所需之樣本數
  • (74,055)SAS輕鬆入門（一）--晨晰統計張顧問整理
  • (67,146)重要-表現程度分析法~Importance- Performance Analysis，IPA(上)
  • (48,319)SAS簡易教學～共變異數分析（Analysis of Covariance, ANCOVA）
  • (47,866)廣義估計方程式（Generalized estimating equation, GEE）簡介~广义估计方程式（GEE）简介---晨晰統計林星帆顧問整理
  • (26,663)醫學篩檢（Medical screening）II－陽性概似比與陰性概似比（Positive and Negative likelihood ratio）~晨晰統計林星帆顧問整理
  • (24,201)使用SPSS之GEE分析處理兩組前後測的介入性研究(上)
  • (10,178)結構方程模式的優勢與劣勢（Advantage and Disadvantage of Structural Equation modeling, SEM）－上（簡介篇）

文章分類

  • power BI (59)
  • 生物醫學統計 (157)
  • 迴歸與SEM (59)
  • 研究方法 (71)
  • SAS教學 (54)
  • Excel與統計軟體 (86)
  • 統計應用專題 (80)
  • 其他類統計知識 (120)
  • 問卷知識 (26)
  • 論文寫作 (17)
  • 統計分析新趨勢 (23)
  • 晨晰的宣傳與服務專案 (62)
  • 數據話視頻 (15)
  • 會員心得分享 (10)
  • 新聞類 (65)
  • 我們的故事 (78)
  • 未分類文章 (1)

最新文章

  • 醫學研究使用PowerBI的情境3—醫療決策系統
  • 醫學研究使用PowerBI的情境(2)—介入措施
  • 紙本問卷鍵檔自己做（二）
  • 紙本問卷鍵檔自己做（一）
  • 醫學研究使用PowerBI的情境(1)—製作圖表
  • 結構方程中介分析-透過AMOS採拔靴法(Bootstrap法)（下）
  • 結構方程中介分析-透過AMOS採拔靴法(Bootstrap法)（上）
  • 一同研究，共同成就!
  • 時間相依Cox model：以生物製劑對帶狀皰疹風險之影響為例
  • 如何在SPSS裡安裝中介調節Marco: PROCESS（2025更新）

最新留言

  • [26/01/23] rechal15 於文章「結構方程中介分析-透過AMOS採拔靴法(...」發表了一則私密留言
  • [25/07/15] 訪客 於文章「專業還是神棍...」留言：
    台灣最新詐術~你是否發現最近怪事一羅匡～{生意倒店｝諸事不...
  • [25/04/25] Lucky Nina 於文章「縱貫型資料用Excel填補空白欄位...」留言：
    這篇文章提供了縱貫型資料處理的完整步驟，詳細解釋了如何利用E...
  • [25/03/05] 西班牙蒼蠅水 於文章「使用SPSS合併資料(merge dat...」留言：
    巴黎偉姐 https://www.tw9g.com/good...
  • [25/02/24] ckhou1 於文章「無母數分析-兩組獨立樣本檢定(Mann-...」留言：
    請問有spss資料檔案嗎? ...
  • [24/12/30] 一 於文章「SPSS進行單因子變異數分析(One w...」留言：
    請問N.S.是什麼的縮寫？謝謝！...
  • [24/12/27] 男性增大液 於文章「誰說Power BI沒有硬核的分析功能？...」留言：
    NAISC延時噴劑 https://www.tw9g.com...
  • [24/12/27] 外用持久液 於文章「SPSS操作成對樣本t檢定（Paired...」留言：
    外用陰莖增大 https://www.tw9g.com/go...
  • [24/10/22] FN 於文章「使用R繪製Survival ROC cu...」留言：
    您好，感謝撰文介紹此套件，感覺非常實用。有個問題想請教，若想...
  • [24/09/15] 頂級偉哥  於文章「KNN（K-Nearest Neighb...」留言：
    美國大陰莖 https://www.tw9g.com/goo...

文章精選

文章搜尋

誰來我家

參觀人氣

  • 本日人氣：
  • 累積人氣：

留言板