三、SPSS讀取Excel檔：
- 10月 20 週一 202510:40
紙本問卷鍵檔自己做（二）
三、SPSS讀取Excel檔：
- 10月 08 週三 202515:37
紙本問卷鍵檔自己做（一）
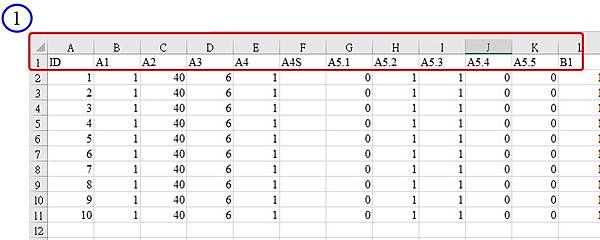
第一次進行量化研究的人，通常會選擇問卷作為研究工具，透過發放紙本問卷來回收資料，接下來就要進行鍵檔，把手邊的紙本問卷轉成電子化資料檔，以利後續的分析進行。這篇文章將舉例一些常見的題型，介紹如何製作Excel表單及鍵入規則。
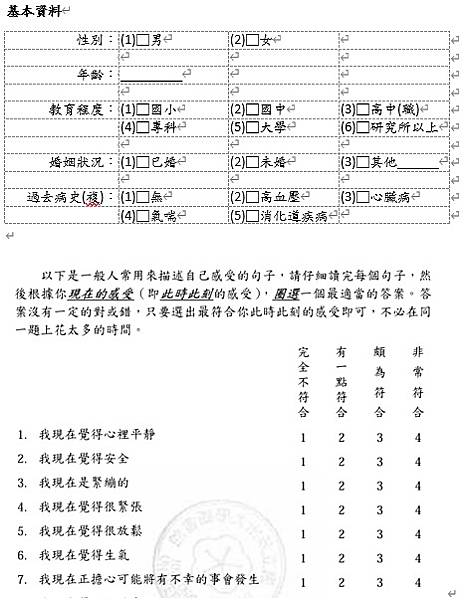
本次的示範題目包含基本資料5題，以及焦慮量表7題，格式如下圖，第一部分的基本資料題目中，性別與教育程度為單選題，代表每位受試者只能選擇一個選項，年齡為數字開放題，婚姻狀況亦為單選題，不過第三個選項其他後面附帶文字開放題，最後一題病史為複選題，代表可以選擇2項以上的選項；第二部分為量表題目，量表題型通常會共用一樣的選項，而選項數為3到7個選項不等，最常見為5個選項，選項為程度上的區別。
- 6月 23 週一 202509:42
如何在SPSS裡安裝中介調節Marco: PROCESS（2025更新）
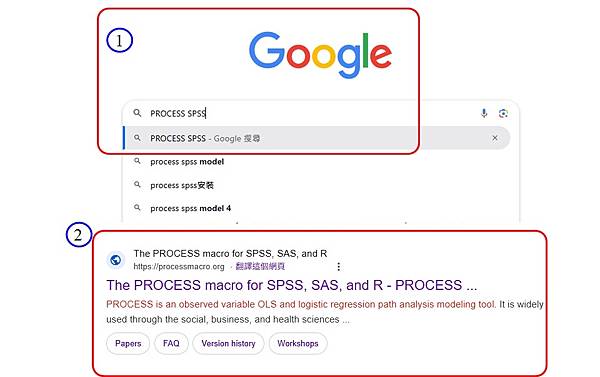若是透過SPSS軟體進行調節分析，現階段最受歡迎的就是使用巨集Marco: PROCESS，甚至客戶每次來就直接指定說：我要跑PROESS，儼然成為中介分析的代名詞，過去文章在進行詹森內曼法的教學時（2017年），已經有提到關於PROCESS的安裝方式，過了這麼多年，才發現不但安裝的選單變了，就連下載的位置也變了，所以更新安裝說明，方便大家使用。
- 5月 26 週一 202509:18
GEE分析介入效果之效果量
近年來關於準實驗設計的研究，大多數都會採用廣義估計方程來分析研究結果，這部分在過去文章有過詳細教學，最後是透過交互作用項的顯著性作為介入成效的判斷依據，其方式是去比較兩組的前後測改變量，因此若我們想要根據這個結果去計算效果量，只需要準備各組別在改變量的平均數即標準差即可，無論是多組別或多個測驗時間點都可以執行，不過由於進行廣義估計方程GEE所使用的資料為長資料格式，但進行改變量的計算需要使用短資料格式，因此先進行長短資料格式的轉向，這部分的操作可先參考過去文章。（https://dasanlin888.pixnet.net/blog/post/323995298）
- 5月 12 週一 202509:24
無母數的兩組獨立樣本檢定-中位數檢定
前陣子有分享「曼－惠特尼U考驗」（Mann-Whitney U-test），這是無母數分析最常使用的兩組獨立樣本檢定，每當檢定結果達顯著水準時，此時問題就來了，該如何去判斷兩組的高低呢?，如果用平均數似乎也有點奇怪，畢竟是放棄了平均數比較法而採用無母數分析，由於是比較兩組的分布，因此以四分位數的Q1 & Q3進行判斷最為合理，不過有時候仍會出現兩群擁有相同的四分數位，那就尷尬了，因此這裡要介紹另一種無母數的兩組比較-中位數檢定，和獨立樣本t檢定以平均數作為比較基準一樣，在中位數檢定即是以中位數進行分組，再比較兩群體在中位數之上或下的比例是否存在差異，其原理是以交叉表的卡方檢定進行分析。
- 4月 09 週三 202514:57
無母數相關分析-Spearman等級相關
提到要進行變項間的相關分析，第一直覺會聯想到皮爾森積差相關（Pearson product-moment correlation），但畢竟是有母數統計，偶爾遇到某些情況被要求改用無母數的相關分析，包含（1）變項不服從常態（2）樣本數小（3）其中一變項為順序尺度，此時將採用Spearman等級相關來探討變項之間的相關情形。
- 3月 10 週一 202509:23
縱貫型資料用Excel填補空白欄位
當縱貫型研究要進行GEE或HLM時，首先我們必須將資料集的格式整理成縱貫型資料（也就是長資料格式），此時每位樣本的每一次資料為一筆資料，若樣本重複測量3次就會有3筆資料，若重複測量5次就會有5筆資料，以此類推，資料格式整理完會像下方圖形一樣，此時變項通常會有4種類型，第一種是辨識變項（如ID、Name），用來辨識每一筆資料的來源；第二種是時間變項（如Time），用來辨識同樣本每筆資料的順序，有些研究也會登錄收案時間點；第三種是固定變項（如性別、年齡），不會隨著時間變動的變項，每次收案的數據皆相同；第四種是相依變項（如albumin），會隨著時間變動的變項，每次收案的數據並不相同。
- 2月 24 週一 202509:12
無母數分析-兩組獨立樣本檢定(Mann-Whitney U-test)（二）
新版介面操作：
（9）若使用新版介面進行無母數分析，必須先設定好變項的尺度，分組變項必須設定為名義，而檢定變項可以是次序或尺度。
- 2月 08 週六 202516:06
無母數分析-兩組獨立樣本檢定(Mann-Whitney U-test)（一）
當要進行兩組的分數比較時，最直覺的聯想就是進行獨立樣本t檢定，歸類在有母數的推論性統計，之前文章提到過，進行獨立樣本t檢定前有三項假設需先符合：（1）常態性、（2）樣本獨立性、（3）變異數同質性。其中樣本獨立性在抽樣適宜的情況下，大致都能符合，但常態性與變異數同質性就得看資料的狀況，透過檢驗才會知道，通常在樣本數小時容易違反。因此就會發現在某些情況下（包含小樣本、依變項不符合常態、依變項為順續變項）時，不太適合有母數統計，而必須改用無母數分析。
- 12月 23 週一 202409:18
使用SPSS分割並儲存為檔案
當研究要針對不同族群對象進行分析時，可以使用資料功能列中的「選取觀察值」或「分割檔案」來進行，不過由於「選取觀察值」是在條件中選取每一組的對象出來分析，並不是像「分割檔案」可以一次輸出個別組別的資料，因此以「分割檔案」的效率表現較佳，這部分的操作說明，可以參考過去的教學文章，網址如下。https://dasanlin888.pixnet.net/blog/post/569598584
